Week6

Nearest neighbor regression

• 資料有可能在不同區段有不同的關係存在

• 當我們要預測一個x的value時，選擇資料中和x最接近的並將其value作為預測結果，這個方法稱為1 Nearest Neighbot (1-NN) regression。

• 如果只有一個Feature，距離很好計算，就是用兩者相減後的絕對值表示(Euclidean Distance)

• 如果有多個Feature，那就針對各個Feature根據重要性給予權重，以下列公式計算(Scaled Euclidean Distance)：

• 用圖形化來表示1-NN (Voronoi Tessellation/Diagram) 
• 把空間分成N個區域，每個區域裡面只有一個資料點Xi
• 在任一區域裡面的點X最近的資料點一定是該區域的資料點
• 對距離有不同定義，則會產生出不同結果的圖

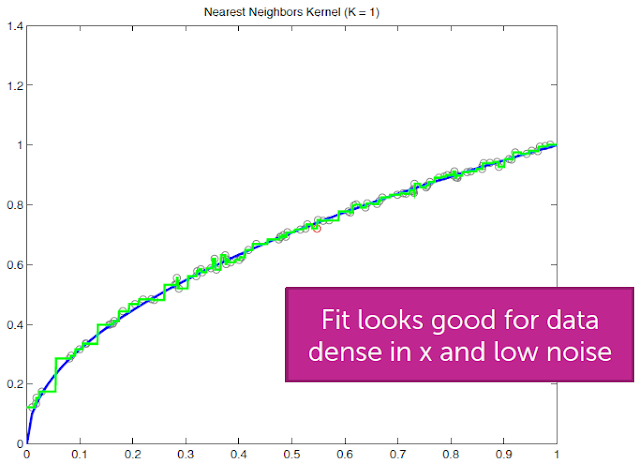
1-NN Algorithm

• 演算法如下，找出和所query的東西最相近的結果

• 當資料量大而且Noise很小時預測結果會很準確

• 在資料間隔比較大的地方會失準

• 若Noise很大，則結果看起來像是Overfitting

k-Nearest neighbors

• 前面提到1-NN在Noise較大時會有失準的問題，所以若能擴大計算預估值的比較資料Set比較能平衡Noise的問題。
• k-NN Regression
• 我們可以找出最接近的k個資料，計算其平均值來當作預測結果
• k-NN Algorithm
• 首先將前k個資料做距離的排序後放到一個Array
• 從第k+1個開始到第N個資料，若比第k個資料的距離還近的話就把該資料插入到Array中
• 最後就可以求出最接近的k個資料

• 下圖說明使用k-NN可以減少Noise造成的影響
• 但在左右兩邊邊界由於取的k個資料都會一樣，所以會變成相同預測值的水平直線
• 資料量少的區域也一樣會有失準的問題

• Discontinuities
• 還有一個問題就是預測的結果不是連續的，當X的單位只改變1時，有可能會造成相差很多的結果。
• 在某些應用下不能太相信此種結果，例如範例中的房價預測。

Weighted k-NN

• 為了解決前面提到不連續的問題，我們可以把這k個結果分別取權重讓預測值更準確及smooth。

• 要怎麼決定權重呢?
• 距離越小者權重越高
• 距離越大者權重越低
• 最簡單的方式就是將權重設成
• 1/距離


• Kernel weights for d=1
• 其他有一些比較複雜的設定權重方式統稱為kernel weight
• Gaussian kernel是其中一個例子
• 𝜆可用來設定smooth的程度
• 它比較特別的是權重永遠不會是0

• Kernel weights for d≥1
• 和d=1的差別在於所帶入的距離函式

Kernel Regression

• 不是只在NN中取權重，而是把所有的Data Point都取權重
• 稱為Nadaraya-Watson kernel weighted average

• 下圖是以Epanechinikov Kernel為例
• 所選擇的Kernel會限定一個區域(圖中黃色部分)，只有在這個區域內的資料才會拿來計算

• 𝜆的選擇比Kernel的選擇還重要!
• 𝜆代表的是所限制的區域大小(Bandwidth)
• 𝜆太小(如圖最左)仍然會有Overfitting造成Variance增大
• 𝜆太大(如圖最右)又過於平滑造成Bias增大
• 𝜆的選擇也是Bias-Variance Tradeoff

• 𝜆和k的選擇最好的方式
• Cross Validation

Formalizing the idea of local fits

• Global constant fit
• 𝜆=1且所有Data Point的權重都一樣
• 結果就會是一條水平直線

• Locally constant fit
• Kernel Regression屬於此種
• Local Regression
• 目前討論的都是locally在每個點去fit constant function
• locally weighted averages
• 若我們想locally在每個點去fit line/polynomial呢?
• locally weighted linear regression
• local linear fit
• 減少邊界的bias但稍微增加variance
• local quadratic fit
• 對邊界問題無用且會增加variance
• 減少邊界外中間區域的bias
• 單數degree的polynomial會比偶數degree好
• 最建議的選擇:
• local linear regression

Discussion on k-NN and kernel regression

• Nonparametric regression
• Nonparametric的目標
• 有彈性
• 對f(x)只要做少量的假設
• 複雜度會隨著觀測資料數量N增加而跟著增加
• k-NN及kernel regression即為此種
• 其他還有Splines, trees, locally weighted structured regression models…
• Noiseless setting
• 若資料皆沒有Noise
• 隨著資料量越來越多
• 1-NN Fit的MSE越來越小
• 當資料量到無限多
• 1-NN Fit的MSE趨近0
• Quadratic Fit則是就算資料量到無限多，仍然不可能完全Fit函式，一定會存在Bias

• Noisy data setting
• 當資料量為無限多
• k越大，NN fit的MSE越小，最後也是會趨近0

• Large d or small N
• NN和kernel regression在資料可以覆蓋整個space的情況下運作很好
• 當dimension d越多，需要越多資料數N去覆蓋space
• N = O(exp(d))才有好的performance
• 這也是為什麼parametric model是有其用途的
• Complexity of NN search
• 若是採Brute force search
• 給一個Query point xq
• 掃過x1,x2,…, xN
• 對1-NN來說要做O(N)次的距離計算
• 對k-NN來說是O(Nlogk) [logk是做排序]

k-NN for classification

• 以區分垃圾郵件為例
• Space即為佈滿著已經分好類的email
• Query email可藉由k-NN找出最相似的k個email
• 看這k個email是垃圾郵件較多還是非垃圾郵件較多
• 即可決定此郵件是哪一類